Function should remain real so math√(x^2–1)/mathshould not be equal to zero so math x^2–1 \neq 0/math mathx^2=1/math Or mathx=\pm 1/math AndThe domain and range of the function f= ((1/1x2)) x ∈ R, x ≠ ± 1 are respectively (A) R 1, 1 (∞, 0) ∪ 1, ∞) (B) R, (∞, 0) ∪ 1 f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞) And the range of a function consists of all the second elements of all the ordered pairs, ie, f(x), so we have to find the values of f(x) to get the required range Now we know for this function x5>0 taking square root on both

Find The Domain And Range Of The Function F X X 1 X 2 Brainly In
F x x 1 -3 domain and range
F x x 1 -3 domain and range-To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find domain and range of `f(x)=x/(1x^2)`F(x)=1 if x4>0 f(x)=1 if x4




What Are The Domain And Range Of The Function F X 1 4 X 3 6x 2 5x 4 Brainly Com
SOLUTION find the range and domain f (x)=1/x2 Question find the range and domain You can put this solution on YOUR website!The "" means "such that," the symbol ∈ means "element of," and "ℝ" means "all real numbers" Putting it all together, this statement can be read as "the domain is the set of all x such that x is an element of all real numbers" The range of f (x) = x2 in set notation is R {y y ≥ 0} R indicates rangeFind the Domain and Range f (x)= (x1)/ (x1) f (x) = x − 1 x 1 f ( x) = x 1 x 1 Set the denominator in x−1 x1 x 1 x 1 equal to 0 0 to find where the expression is undefined x1 = 0 x 1 = 0 Subtract 1 1 from both sides of the equation x = −1 x = 1
Algebra Find the Domain and Range f (x)=x^21 f (x) = x2 1 f ( x) = x 2 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationQuestion 1 Find the domain and range of the following functions f(x) = x 3 Solution Domain A set of all defined values of x is known as domain Range The out comes or values that we get for y is known as range Domain for given function f(x) = x 3 For any real values of x, f(x) will give defined values Hence the domain is R Misc 4 Find the domain and the range of the real function f defined by f(x) = √((𝑥−1)) It is given that the function is a real function Hence, both its domain and range should be real numbers x can be a number greater 1 Here, f(x) is always positive, Minimum value of f(x) is 0,
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeFirst week only $499!See Answer Check out a sample Q&A here Want to see this answer and more?




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2
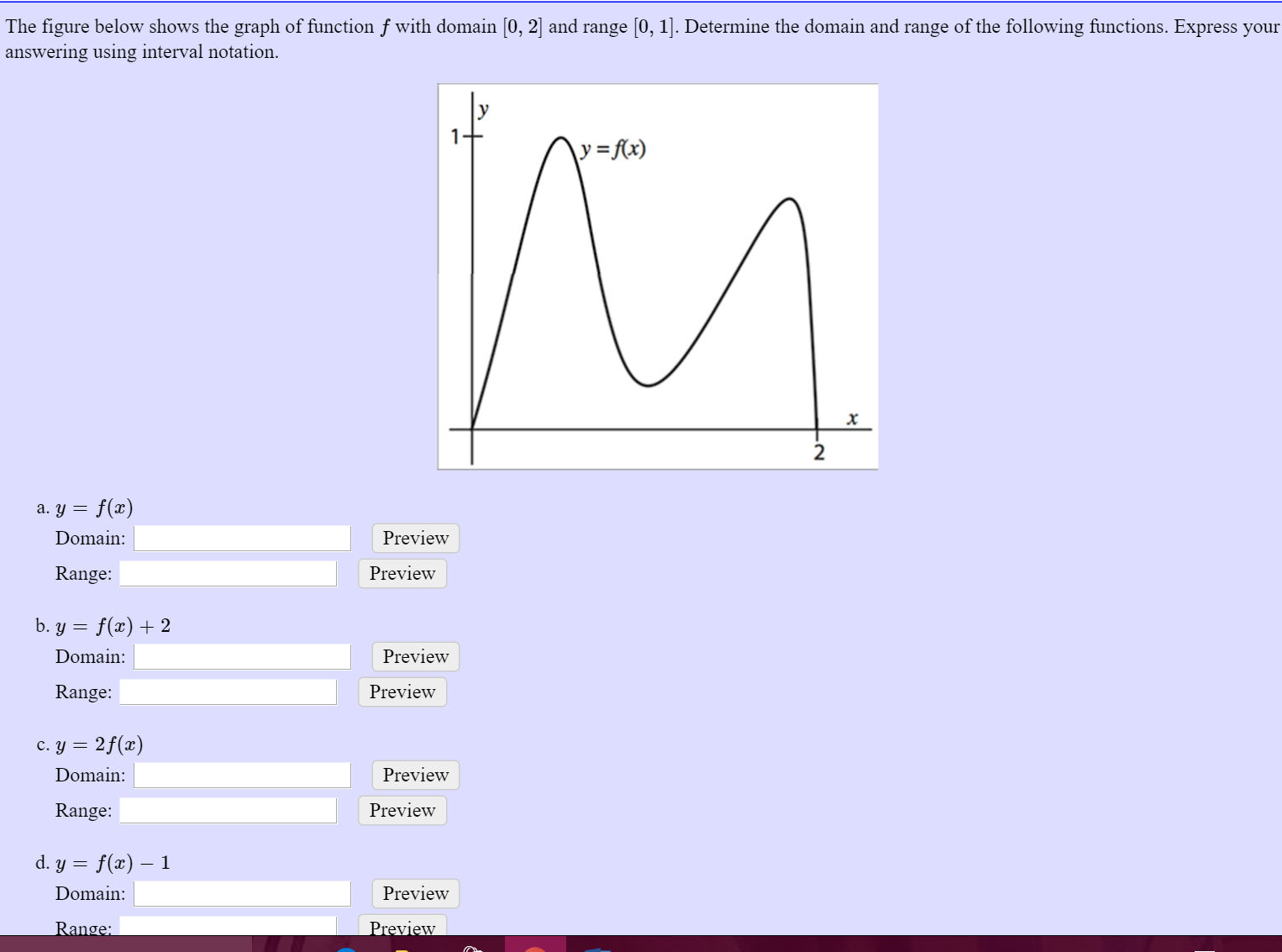



The Figure Below Shows The Graph Of Function F With Chegg Com
The domain and range are the intervals in which the function is defined in the x and y axes Answer and Explanation 1 We are given the function {eq}f(x)=2x^23x1 {/eq}(0, infinity) , {x/x > 0) for any integer Range;Find the Domain and Range f (x)=1 f (x) = 1 f ( x) = 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x



How Do You Graph F X 2 X 1 3 And State The Domain And Range Socratic




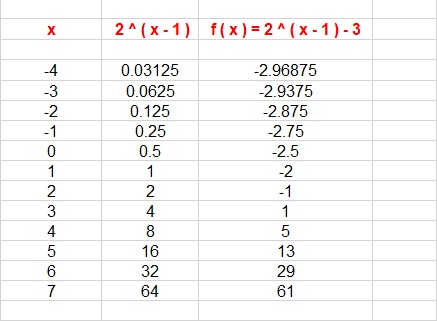
The Problem Was To Graph The Function Find The Chegg Com
Domain is all reals except 1 (Can't divide by 0) Range if y=1/(x1), then y(x1)=1 son xyy=1 and xy=1y, finally, then x=(1y)/y y can take any value except 0 Range is all reals except 0 graph{y=1/(x1) 974, 803, 38, 509}Find Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)`Arrow_forward Question View transcribed image text fullscreen Expand check_circle Expert Answer Want to see the stepbystep answer?
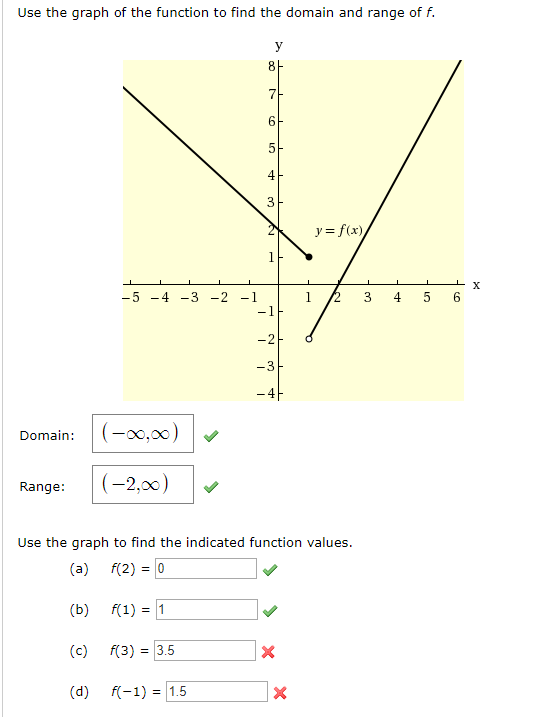



Use The Graph Of The Function To Find The Domain And Chegg Com




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2
Were given a function and we're asked to find the domain and range of dysfunction Function is F of X equals one plus X square Notice that the function F is a polynomial function that's a quadratic function and therefore the domain of F is all real numbersActually, at first glance, I don't know So I have to break this down into parts that I do know tan(x) = sin(x) / cos(x) And I know 1/tan(x) = cos(x)/sin(x), so to find the domain I have to look for the places where the denominator is zero (first114 Range of a function For a function f X → Y the range of f is the set of yvalues such that y = f(x) for some x in X This corresponds to the set of yvalues when we describe a function as a set of ordered pairs (x,y) The function y = √ x has range;
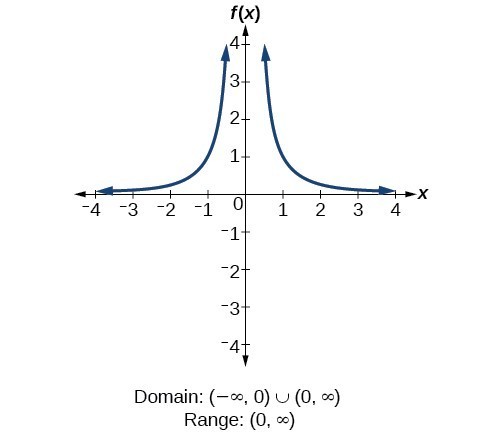



Determine Domain And Range From A Graph College Algebra
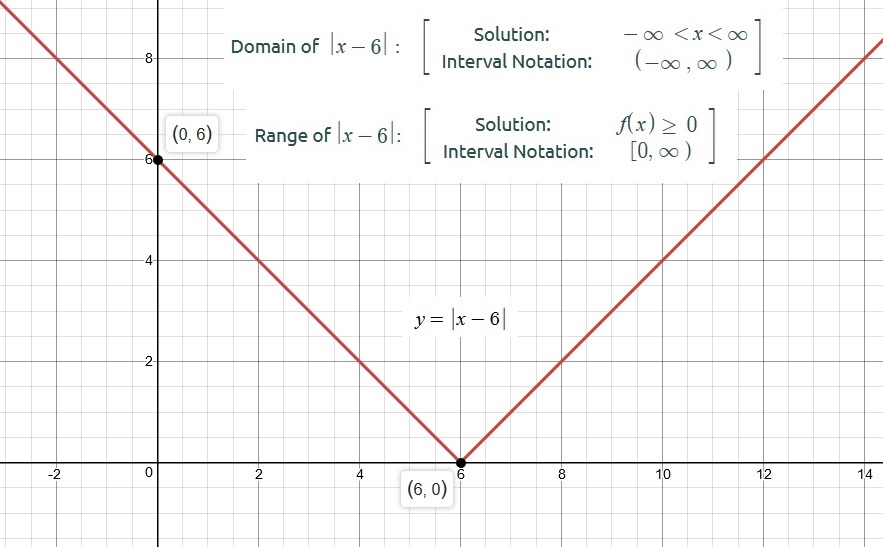



How Do You Find The Domain And Range Of Y X 6 Socratic
Transcript Misc 6 Let f = {("x, " 𝑥2/(1𝑥2)) x ∈ R } be a function from R into R Determine the range of f f = { ("x , " 𝑥2/(1𝑥2)) x ∈ R } We find different values of 𝑥2/(1 𝑥2) for different values of x Domain Value will always be between 0 & 1 We note that Value of range y = 𝑥2/(1 𝑥2) is always positive Also, it is always between 0 and 1 Hence, Range is 1 Confirm that you have a quadratic function A quadratic function has the form ax 2 bx c f (x) = 2x 2 3x 4 The shape of a quadratic function on a graph is parabola pointing up or down There are different methods to calculating the range of a function depending on the type you are working withAnswer and Explanation 1 Given f(x) = 1 x f ( x) = 1 x Domain Since the function is a fraction, the value of the variable are all real numbers except 0 0 since it will result to an undefined
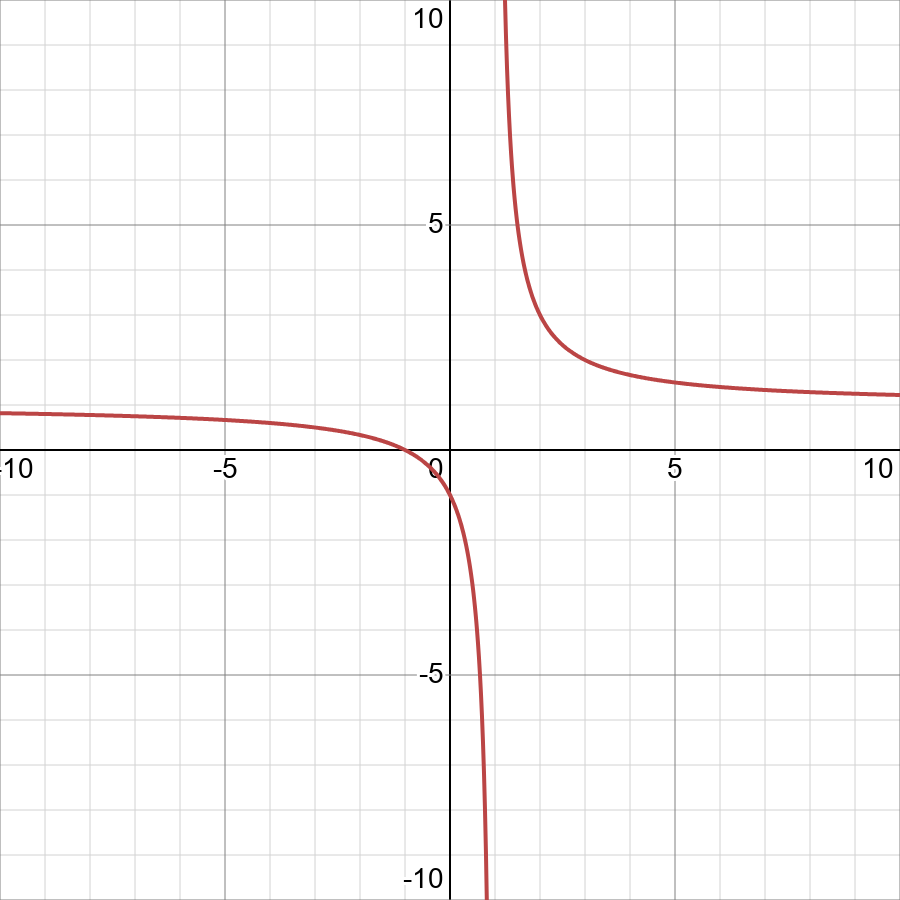



Find The Domain And Range F X X 1 X 1 Displaystyle Fleft Xright Frac X 1 X 1 Snapsolve




Find The Domain And Range Of The Function F X 1 Sqrt X 5 Youtube
Click here 👆 to get an answer to your question ️ For the function f(x) = 3(x − 1)2 2, identify the vertex, domain, and range The vertex is (1, 2), the dom All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f(x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f(x) = √((9 −x^2)) It is given that the function is a real functionFunction, Domain, Range and Inverse Function Part 3 of 3 ExamplesHelp your child succeed in math at https//wwwpatreoncom/tucsonmathdoc




How To Find The Domain And Range Of A Function 14 Steps
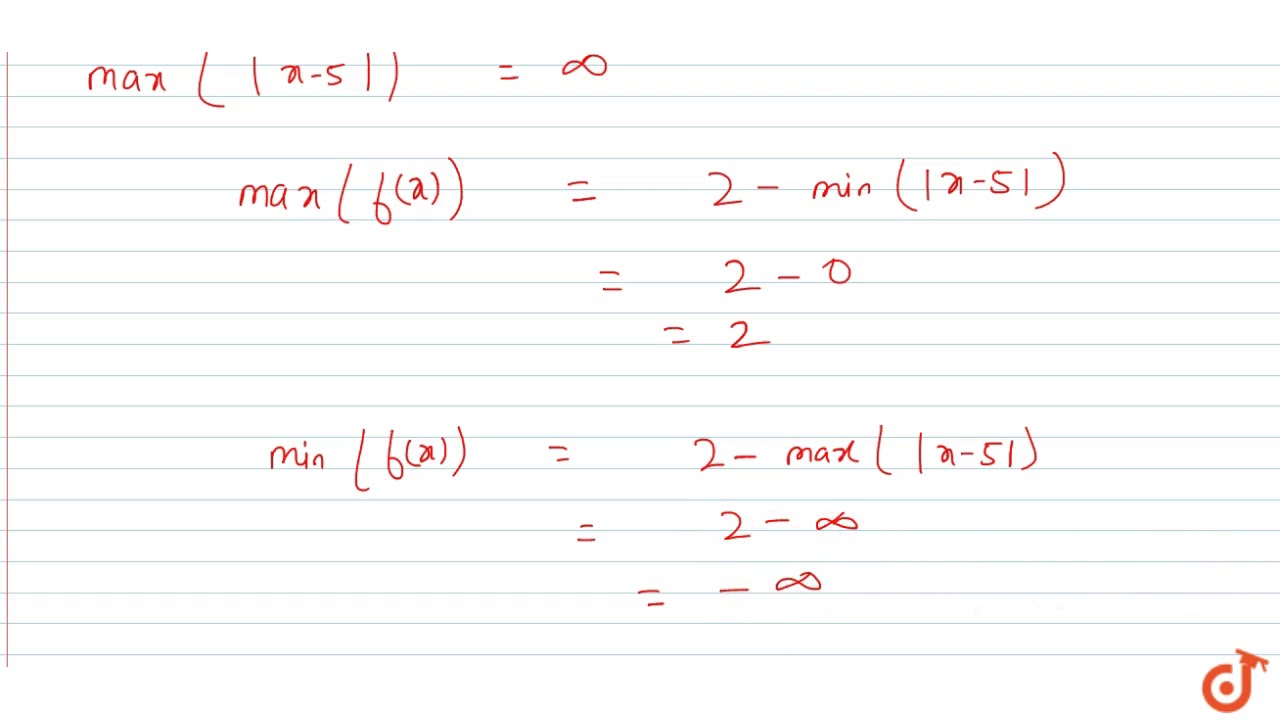



The Domain And Range Of The Function F Given By F X 2 X 5 Is Youtube
Domain and Range of Exponential and Logarithmic Functions Recall that the domain of a function is the set of input or x values for which the function is defined, while the range is the set of all the output or y values that the function takes A simple exponential function like f(x) = 2x has as its domain the whole real lineArithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution f(x)=\frac{1}{x^2} domain\y=\frac{x}{x^26x8} domain\f(x)=\sqrt{x3} domain\f(x)=\cos(2x5) domain\f(x(1, infinity) , {y/y > 1)




What Is True About The Domain And Range Of The Function The Graph Of The Function F X X 2 X Brainly Com
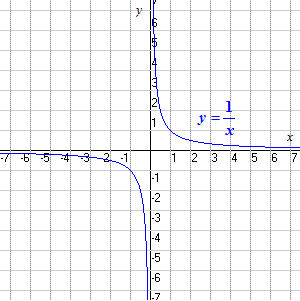



Domain And Range
For example, a function f (x) f ( x) that is defined for real values x x in R R has domain R R, and is sometimes said to be "a function over the reals" The set of values to which D D is sent by the function is called the range Informally, if a function is defined on some set, then we call that set the domainThe domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value1 find the domain and range of f(x) 2 cos3x close Start your trial now!
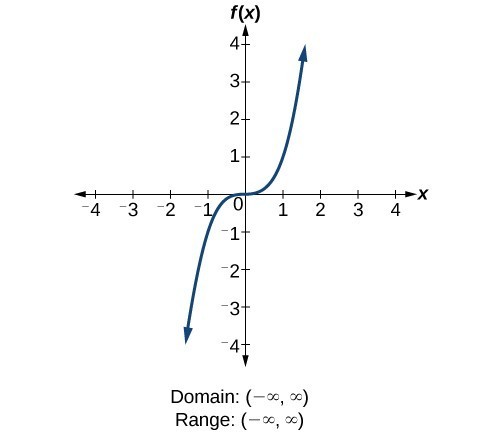



Determine Domain And Range From A Graph College Algebra



What Is The Domain And Range For The Following Function And Its Inverse F X 3x 1 2 Mathskey Com
Domain for f(x) to be a real valued function 49x^2 >=0 49>=x^2 7All real y ≥ 0 Example a State the domain and range of y = √ x4 b Sketch Find domain and range of f(x)= square root of (x 1)(3 x) Enter your answer for the domain using interval notation Set the radicand in greater than or equal to to find where the expression is defined Fx x 2 2 x 1 Solution to Example 3 Let fx4 on the square root of x 1 Identify the domain of the function fx x 3 Thank you very much




How To Find Domain And Range Of The Inverse Of A Relation Sat Math




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube
Set the denominator equal to zero Remember, dividing by 0 is undefined So if we find values of x that make the denominator zero, then we must exclude them from the domain Now to find the range, notice thatAlgebra Find the Domain and Range f (x)=1/ (x1) f (x) = 1 x − 1 f ( x) = 1 x 1 Set the denominator in 1 x−1 1 x 1 equal to 0 0 to find where the expression is undefined x−1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1Find the domain and range of the function `f (x)= (1)/sqrt (x5)` Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up



The Domain And Range Of The Function F X X 2 Is Donimain



What Is The Range Of F X X 1 X 1 Quora
Find the Domain and Range f (x)=1/x f (x) = 1 x f ( x) = 1 x Set the denominator in 1 x 1 x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x that make the expression defined Interval NotationHow to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support Find the domain by finding where the function is defined The range is the set of valves that correspond with the domain Domain;




Domain And Range Of Quadratic Functions Video Khan Academy




What Are The Domain And Range Of The Function F X 1 4 X 3 6x 2 5x 4 Brainly Com
Logarithmic Function The logarithmic function is those expressed in the form ({eq}y=\log_ax {/eq}), where a is the base that must be Transcript Misc 5 Find the domain and the range of the real function f defined by f (x) = x – 1 Here we are given a real function Hence, both domain and range should be real numbers Here, x can be any real number Here, f (x) will always be positive or zero Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that range f (x) is 0 or positive numbers, So range cannot be negative Hence, RangeWhat are the domain and range of f(x) = log(x 1) 2?




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In



3
The answer for the question shown above is the second one, which is The domain is all real numbers The range is all real numbers greater than zero The explanation is shown below You have the following function given in the problem above f(x)= (1/5)^x As you can see, it is a exponential function The range is the set of all valid values Find the domain and range of f (x)=x2/1x2 Domain of the function is where the function is defined The given function X R Let fx y y x1x2 x y1 x2 yx2 x y 0 This is quadratic equation with real roots Find the domain and range ƒx 1 x2 Maintain the following steps 1 Rangeset of values of f(x)/y for given domain Here f(x)=√(x1) We know that root of negative number is not defined (ideally we can take iota ibut we can not take i without being mentioned) So,our X must be greater or equal to 1 Domain is(1,inf) For range put x= 1 minimum value is 0 and maximum can go upto infinite So,range is (0,inf)




Domain Range F 1 All X Such That F X 1 X Chegg Com




The Graph Of F X Is Given Above Determine The Domain And Range Of F 1 X Using Interval Notation Brainly In
For instance, f(x) = itex\frac{1}{x3}/itex The domain is simply the denominator set equal to 0, {xl x≠3} However, range is found by solving for (isolating x to one side) and setting the denominator equal to zero x = itex3\frac{1}{y}/itex So range is {xl x≠0} This is a systematic method that I assume is the only way to find the range Find the domain and range of the real function f(x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f(x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R ️Let f(x) = y ️y = x/1x^2 ️⇒ x = y(1 x^2) ️⇒ yx^2 – x y = 0 ️This is quadratic equation with real roots ️(1)^2 – 4(y)(y) ≥ 0 Given that f(x) = 1/√(x 5) Here, it is clear that (x) is real when x – 5 > 0 ⇒ x > 5 Hence, the domain = (5, ∞) Now to find the range put For x ∈ (5, ∞), y ∈ R Hence, the range of f




Find The Domain Or Range Of Following Function Tex F X Sqrt X 1 3 X Tex Brainly In



Domain And Range Examples Domain And Range Of Functions
We know that element inside the square root should be greater than or equal to zero But in this case since square root is in denominator it can't be equal to zero So in this case element inside the square root should be greater than zero ie




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Let F X Ln X Y 1 Find And Sketch The Domain Of F What Is The Range Of F Study Com




Find The Domain And Range Of F X Root Of X 1 Brainly In
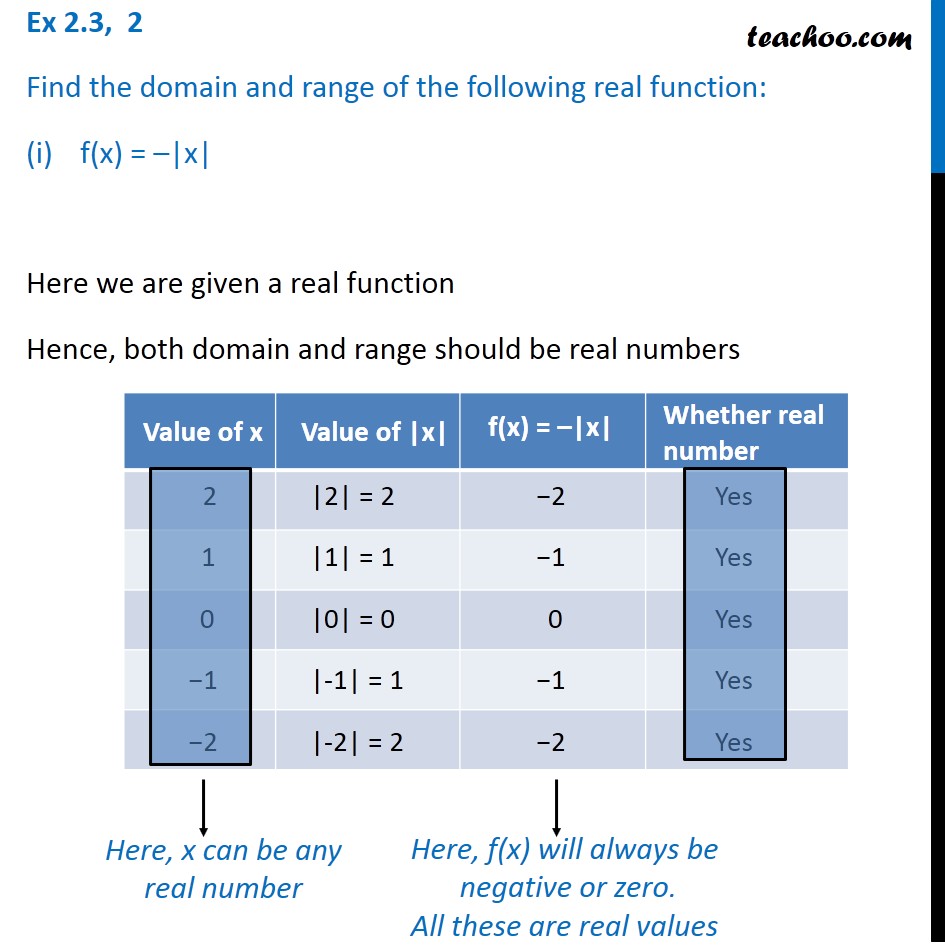



Ex 2 3 2 Find Domain And Range I F X X Chapter 2




Find The Domain And Range Of The Function F R To R F X X 2 1



What Is The Range Of The Function F X X 1 Quora




Domain And Range Of 1 X 2 2x 8 Youtube




Find The Domain And The Range Of The Real Function F Defined By F X X 1
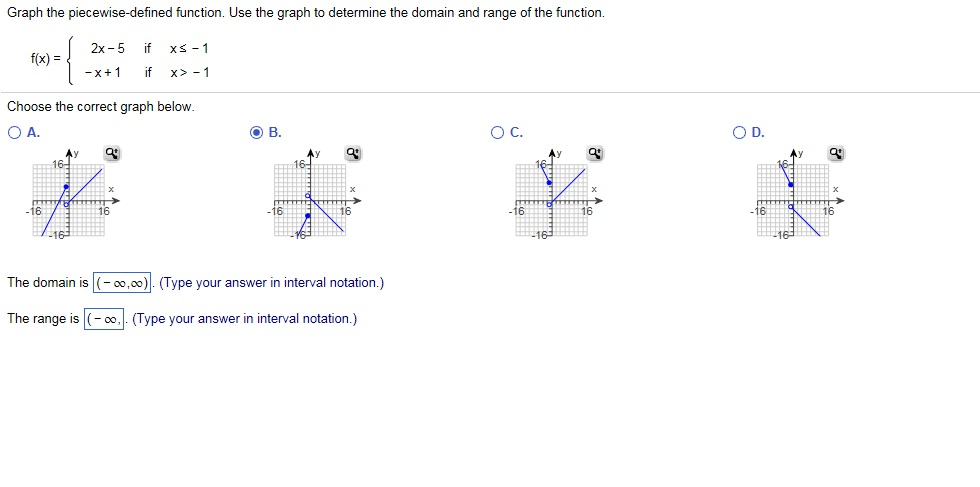



Graph The Piecewise Defined Function Use The Graph Chegg Com




Find Domain And Range Of F X X 1 X 2




Find Domain And Range Of Function Y 1 X Youtube
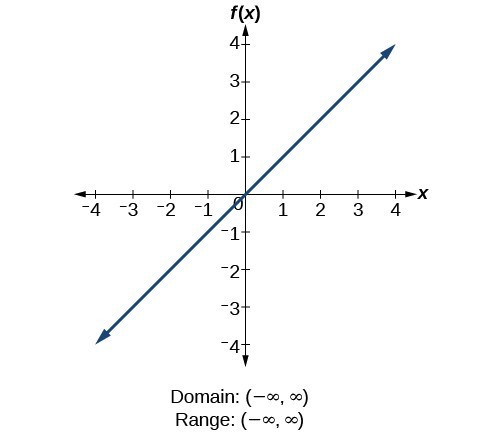



Find Domains And Ranges Of The Toolkit Functions College Algebra




Find Domain And Range F X X 1 X 1 Maths Relations And Functions Meritnation Com




Find Domain And Range Of F X 1 16 X 2 Brainly In



Solution Find The Domain An Range Of F X X 1 X
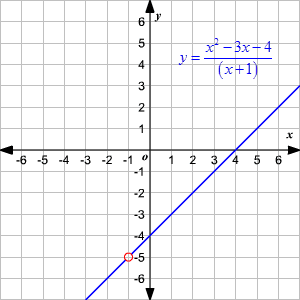



Domain And Range Of Rational Functions



Search Q Domain And Range Table Tbm Isch




Domain Of A Function F X X 1 Is Trendnj




Find The Domain And Range Of The Inverse Of The Given Chegg Com




Answered 6 Determine The Domain And Range Of Bartleby




Find The Domain And Range Of F X X 1 Youtube



Find Domain And Range Of Function Y 1 X Youtube
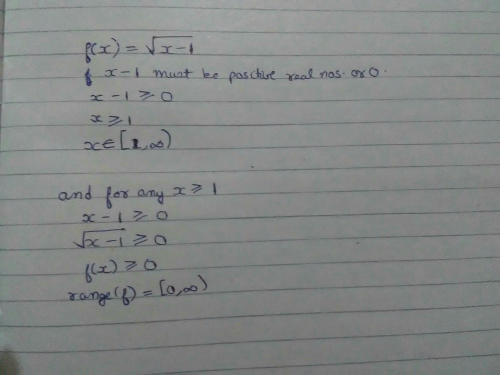



Find The Domain And Range Of Real Function F Defined By F X Underoot Of X 1 Edurev Class 11 Question
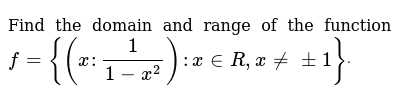



Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot



3 3 Domain And Range Mathematics Libretexts




Find The Domain And Range Of The Function F X Chegg Com



Domain And Range From A Graph A Function F Is Given Chegg Com




Domain And Range Of F X X 3 X 3 Are Respectively




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic



Question Video Finding The Domain And Range Of A Cubic Function Given Its Graph Nagwa
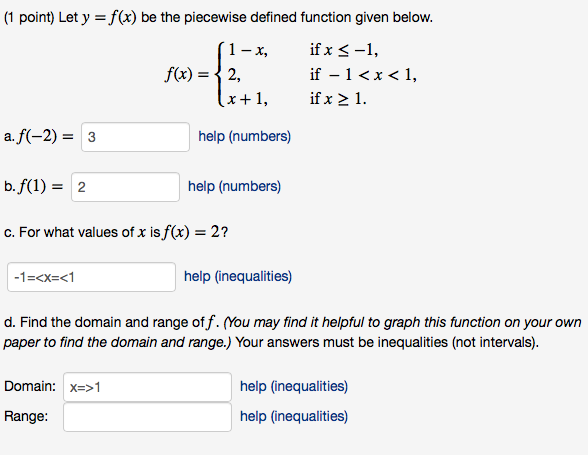



Let Y F X Be The Piecewise Defined Function Given Chegg Com




Find Domain And Range Of F X X 1 C 2x 8 Maths Relations And Functions Meritnation Com
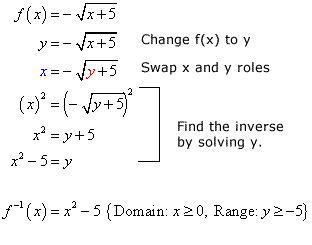



Inverse Of Square Root Function Chilimath
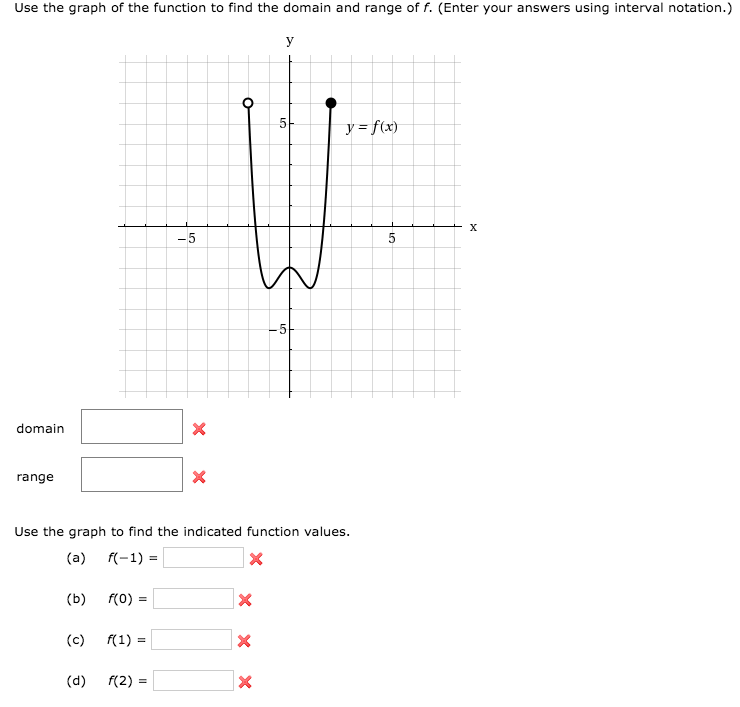



Use The Graph Of The Function To Find The Domain And Chegg Com




How To Find Domain And Range From A Graph Video Khan Academy




9 Find The Domain And Range Of F 1 Where F X X 1 Chegg Com




What Are The Domain And Range Of F X 1 6 X 2 Brainly Com




Find The Domain Range Of F X 1 9 X 2 Brainly In




Find Domain And Range Of Sine Inverse 5x 1 Youtube




Graph F 1 X Identify The Domain And Range Of Chegg Com




F X 2x 1 Find Domain And Range Brainly In




Find The Domain And Range Of The Function F X Sin 1 X 2 2




What Are The Domain And Range Of F X 1 5 X Brainly Com




Consider The Function F X X 1 C 2x 8 2x 8 C X 1 Statement 1 Domain Of F X Is Singleton Statement 2 Range Of F X Is Singleton



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora




Find The Domain And Range Of F X Sin 1 X X Where Represents The Greatest Integer Function
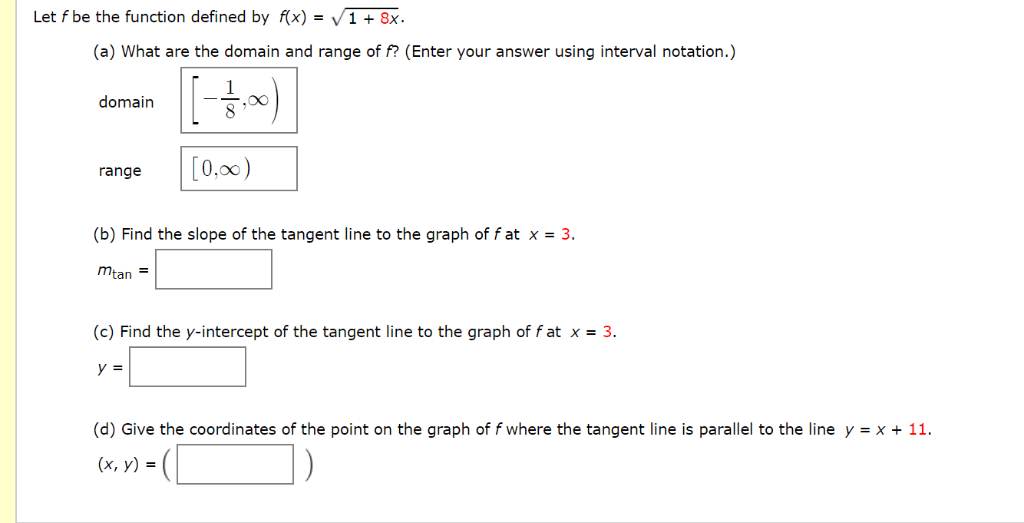



Let F Be The Function Defined By F X 1 8x A Chegg Com
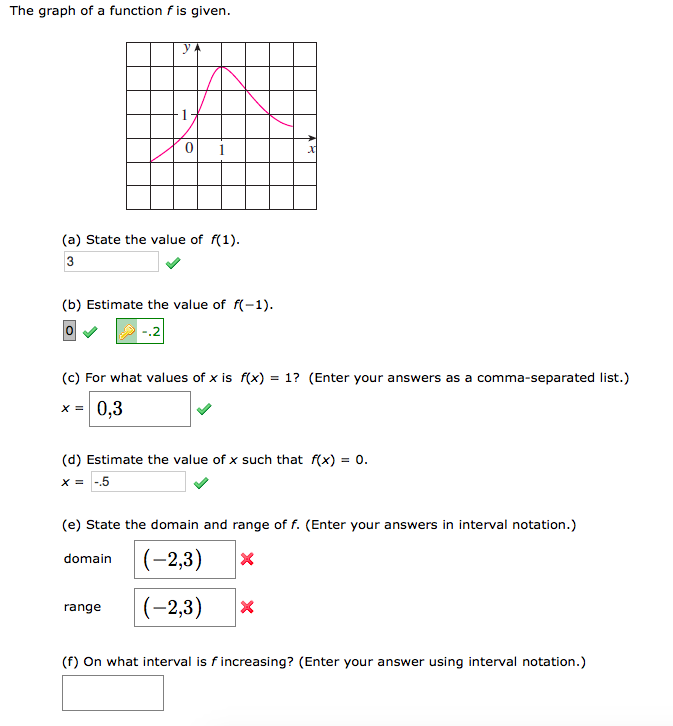



The Graph Of A Function F Is Given A State The Chegg Com




Misc 5 Find Domain And Range Of F X X 1 Class 11
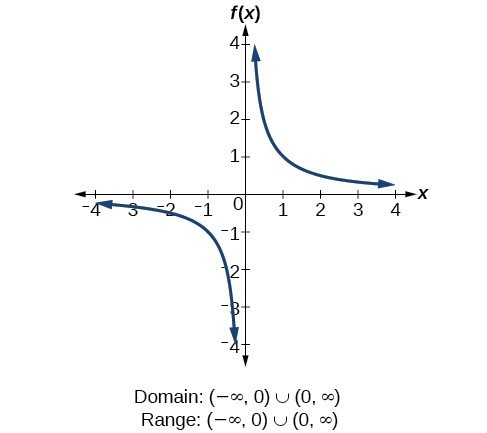



Determine Domain And Range From A Graph College Algebra




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube




Given That F X 1 2x 3 Find F 1 The Domain Of Chegg Com



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora



How Do You Find The Domain And Range Of T 1 3 Socratic



What Is The Range Of The Function F X X 1 Quora




1 4 Pts State The Domain And Range Of F X 1 X Chegg Com




Find Domain And Range Of Function Y 1 X Youtube




Find F X And Identify The Domain And Range Of F 1 Chegg Com



What Is The Range Of F X X 1 X 1 Quora
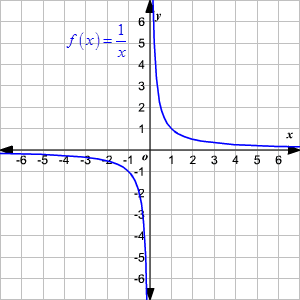



Domain And Range Of Rational Functions



1




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube



What Is The Range Of 1 X 2 1 Quora
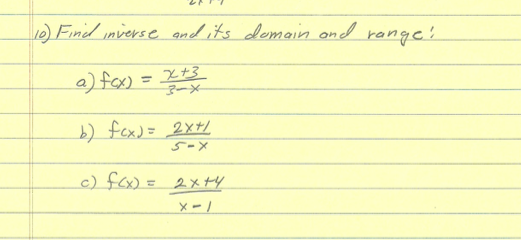



Find Inverse And Its Domain And Range F X X Chegg Com




What Is The Range Of The Function F X X 1 X 1 Youtube
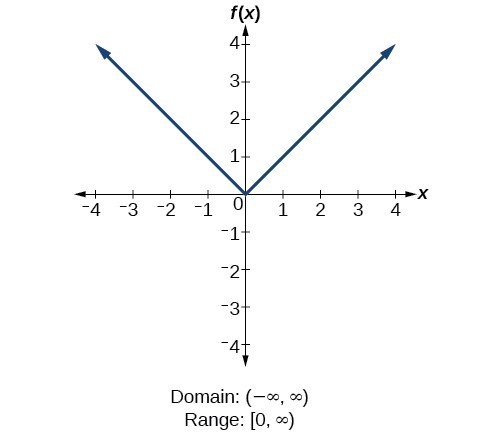



Find Domains And Ranges Of The Toolkit Functions College Algebra



Q Tbn And9gcqgqrwpnxjwt0kskruy6guwbb9vrtxcyvozrczh7yys7zu6fw5a Usqp Cau




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube



What Is The Domain And Range Of X 2 1 X 2 Quora
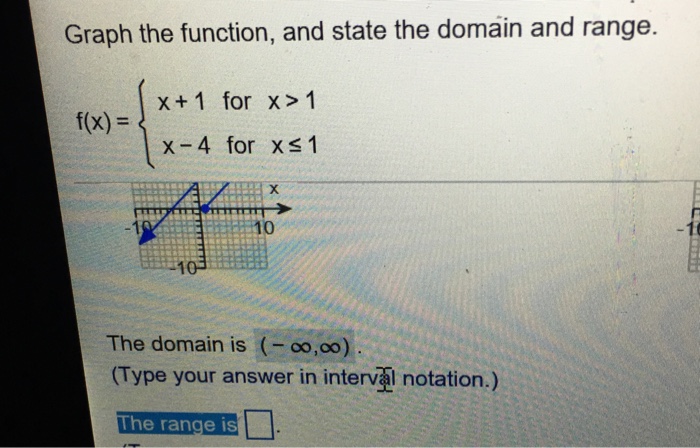



Graph The Function And State The Domain Range F X Chegg Com




If F X X2 1gx X2 1 Find F G X Identify The Chegg Com




Domain And Range Calculator Wolfram Alpha




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot



0 件のコメント:
コメントを投稿