Solution for Graph the level curves in the first quadrant of the xyplane for the following functions at heights of z = 0, z = 2, and z = 4;3x y 2z = 8The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;

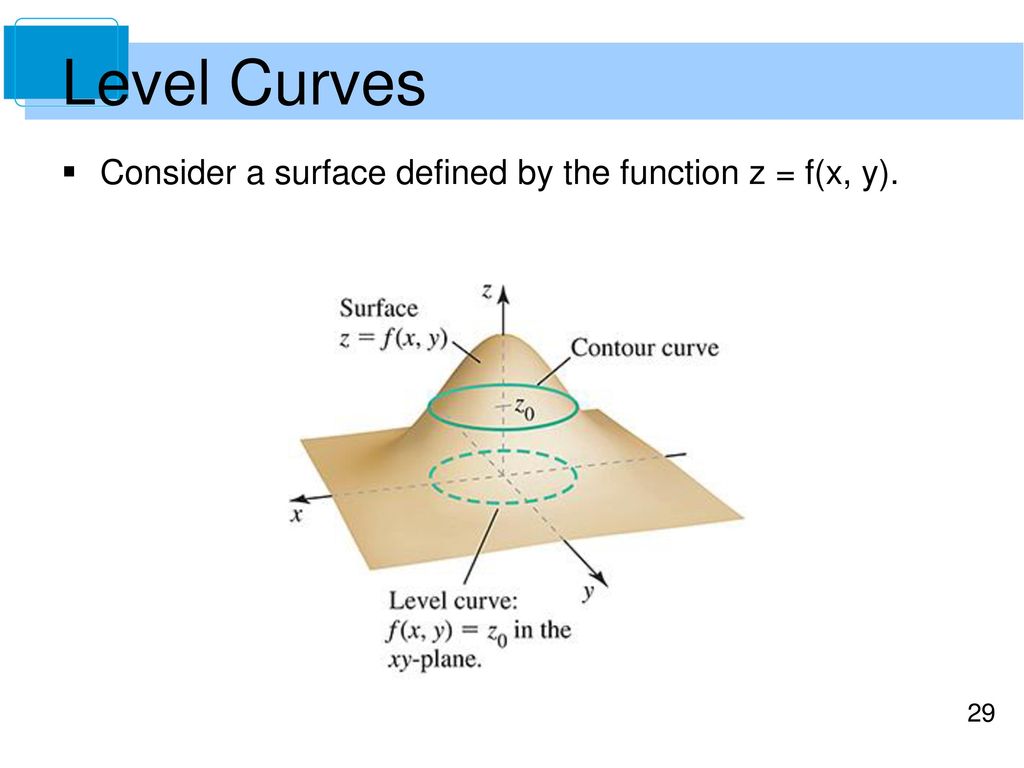
Level Curves
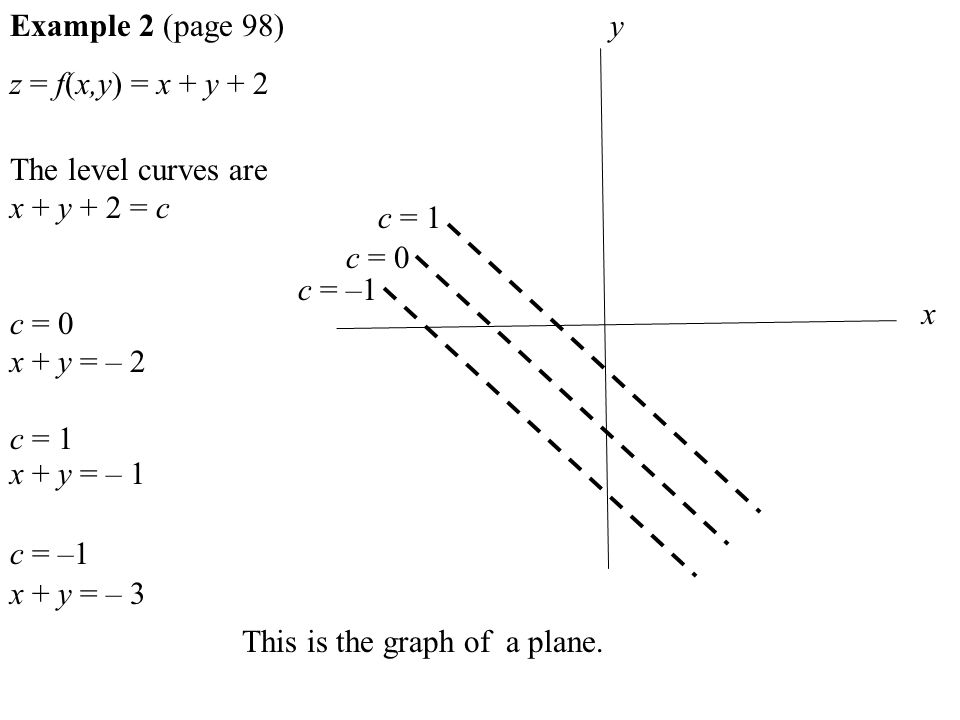
Level curves of a plane
Level curves of a plane-Uploaded By jchen41 Pages 6 This preview shows page 3 6 out of 6 pagesThe level curves F ( x, y) = c are in the range of the function The level curves F ( x, y) = c are on the surface z = F ( x, y) The level curves F ( x, y) = c can also be thought of as the intersection of the plane z = c with the surface z = F ( x, y) We often mark the function value on the corresponding level set


Hyperbolic Paraboloid Geogebra Dynamic Worksheet
K with the surface defined by f Level curves are also known as contour linesThus the curve described by x 2 xy 2 5 is part of a level curve of f x y III Thus the curve described by x 2 xy 2 5 is part of a School Brooklyn Technical High School;Level curves are a way of giving visual information about a surface in R 3 in a 2 dimensional form E xample 1 6 1
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)Y is a twodimensional curve with the equation f x ,The level curves of are curves in the plane along which has a constant value The level surfaces of are surfaces in space on which has a constant value Sometimes, level curves or surfaces are referred to as level sets
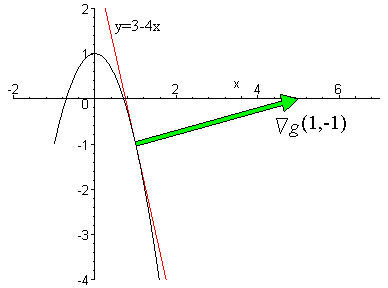
Y is a twodimensional curve with either the equation z =Gradient proof that it is perpendicular to level curves and surfaces Let w = f(x,y,z) be a function of 3 variables We will show that at any point P = (x 0,y 0,z 0) on the level surface f(x,y,z) = c (so f(x 0,y 0,z 0) = c) the gradient f P is perpendicular to the surfaceLevel curves themselves can give us information about the rate of increase The more closely spaced they are, the faster the increase, but by themselves, they cannot tell us whether the curve is increasing or decreasing It's the gradient that gives us that So consider the graph below showing the gradient only What can you tell



Level Curves And Implicit Differentiation Studocu



Level Curves
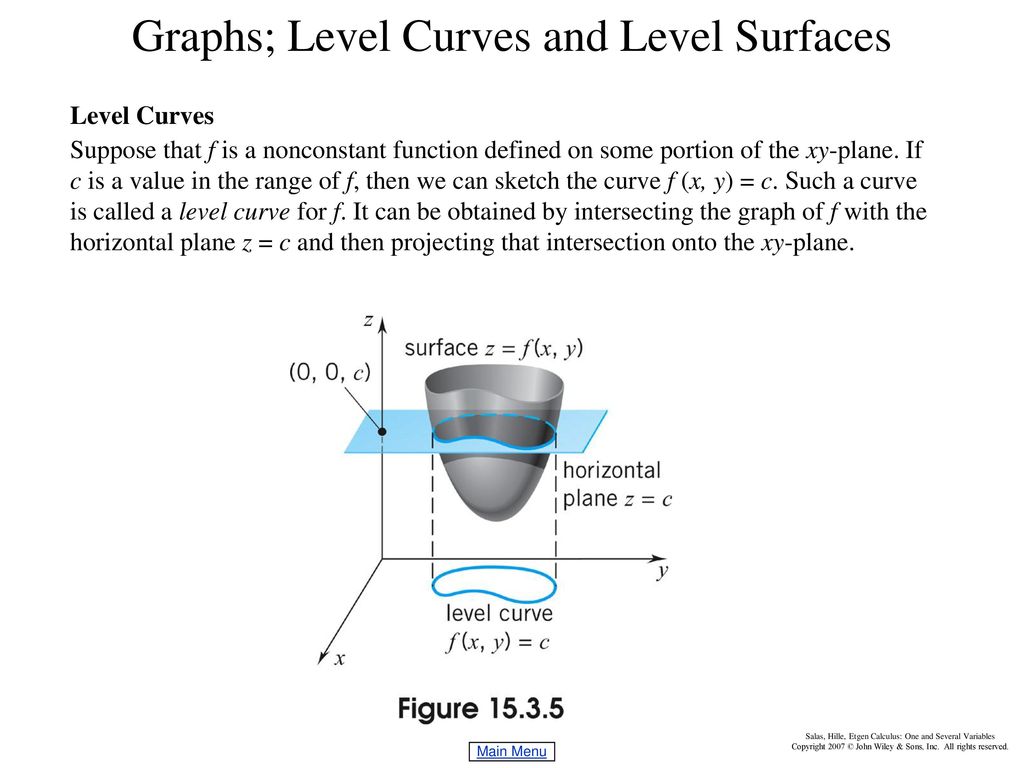
A contour line (also known as a level curve) for a given surface is the curve of intersection of the surface with a horizontal plane, z = c A representative collection of contour lines, projected onto the xy plane, is a contour map or contour plot of the surface In particular, if the surface is the graph of a function of two variables, say z = f ( x, y ), then the contours are defined implicitly by equations of the form f ( x, y ) = c, z = cAnalysis Parameter u is the height z of a contour, so take the first two equations for a fixed value of u, eg ParametricPlot{125 Cosv, 125 Sinv}, {v, 0, 2 Pi} whose result, not shown here, is the expected circle Implementation For several heights, apply a function with the height as argument to a list of those heights, producing a list of individual circular images;The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;



Level Curves Of Functions Of Two Variables Youtube
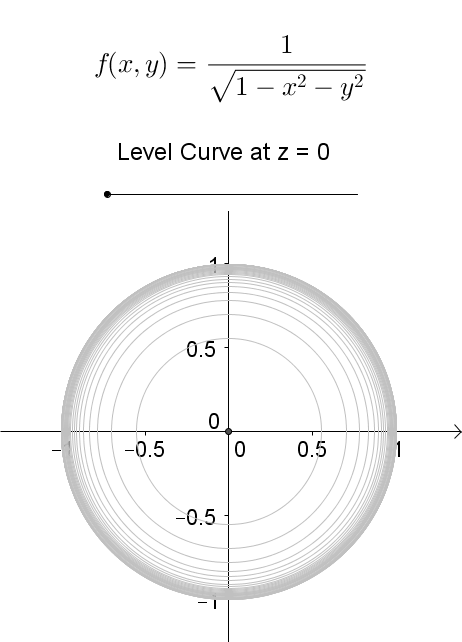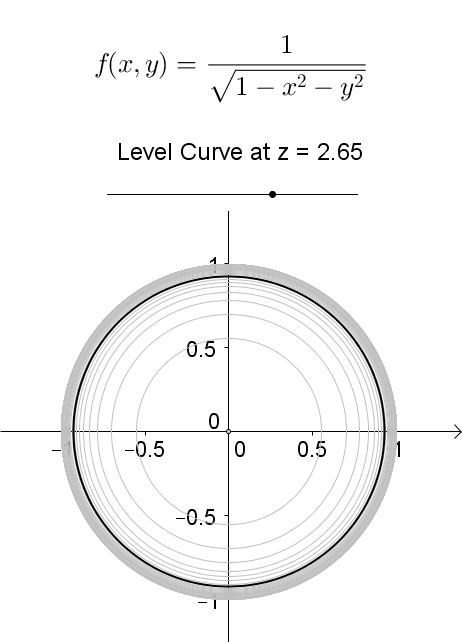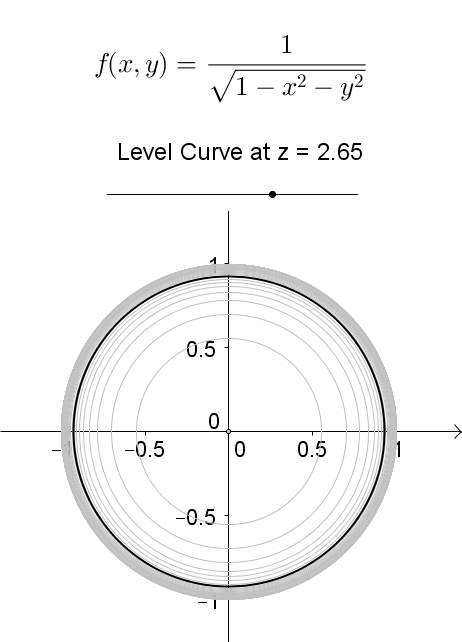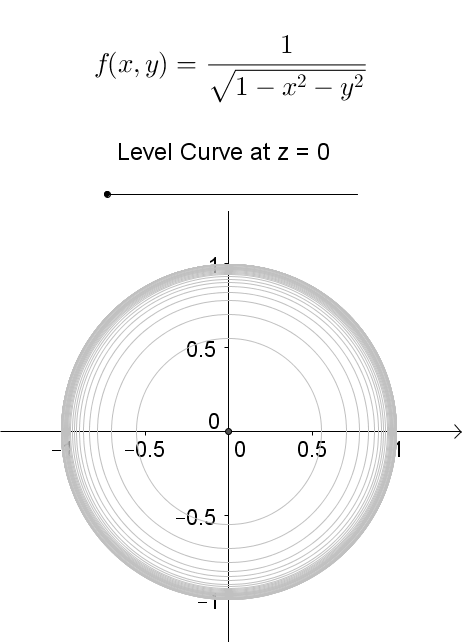


Level Curves Geogebra Dynamic Worksheet
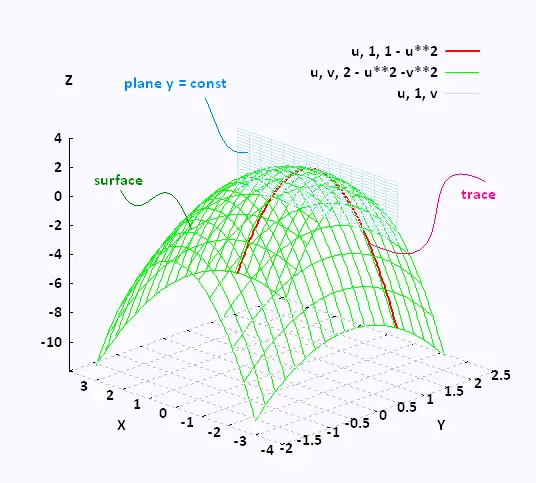
Level Curves and Plane Sections The Cross Section tutor is used to investigate the level curves and plane sections of a surface Alternative Content Note In Maple 18, contextsensitive menus were incorporated into the new Maple Context Panel, located on the right side of the Maple window If you are using Maple 18, instead of rightLevel Curves For a general function z = f ( x, y), slicing horizontally is a particularly important idea Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = cIn this situation, the level curves of S are the (plane) curves which are obtained by intersecting S with planes normal to the zaxis Furthermore, given b ∈ R we will denote the level curve corresponding to the plane z − b = 0 by S b Note that one might similarly define the level curves corresponding to the xaxis and the yaxis, respectively



14 Partial Derivatives Ppt Video Online Download



Consider The Function F X Y 6 32 32 A Determine The Level Curves For The Surface When Homeworklib
$\begingroup$ The map $\b C\to\b R^2$ that takes real/imaginary parts to first/second components will preserve the geometry of figures in the complex plane Like curves, intersections and orthogonality $\endgroup$ – anon May 16 '12 at 21Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy planeThe osculating planes of a curve pass through a fixed point $\rightarrow$ the curve is a plane curve 2 $\alpha$ is a plane curve if and only if all its osculator planes intersect at one point


If X X1 X2 Represents A Point In A Subset A Of Rn And F X Is Exactly One Point In Rm Then We Say That F



15 1 Graphs And Level Curves Youtube
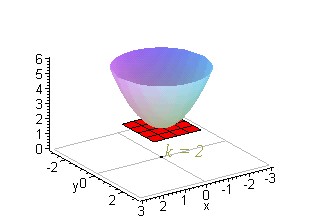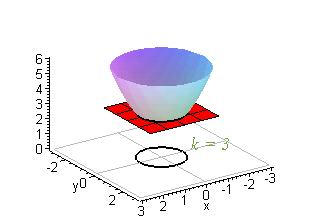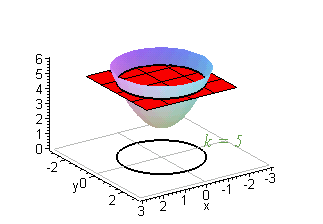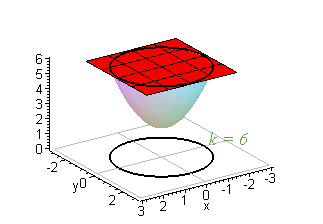
Level Curves Added May 5, 15 by RicardoHdez in Mathematics The level curves of f(x,y) are curves in the xyplane along which f has a constant value Send feedbackVisit WolframAlpha SHARE Email;Then the curves obtained by the intersections of the planes $z = k$, $k \in \mathbb{R}$ with the graph of $f$ are called the Level Curves of $f$ From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$ axis and the surface generated by the function $z = f(x, y)$Show that the level curves for different choices of {eq}k {/eq} form distinct parallel lines in the {eq}xy {/eq}plane Level Curves Recall that the pole in polar coordinates is the{eq}z {/eq}axis


Level Curves And Contour Plots Mathonline



Phase Plane With Some Level Curves Of The Lyapunov Function The Solid Download Scientific Diagram
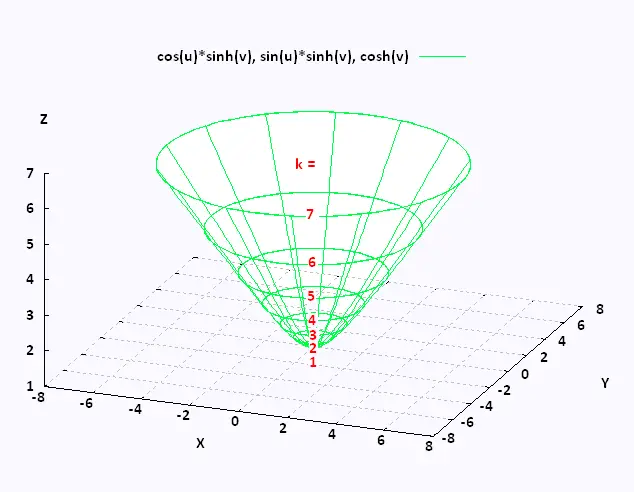
In the simplest case, = 2 2, an intersection of this surface with a plane =𝑘 forms a level curve that is a circle Thus, the contour map of this paraboloid will be concentric circles centered at the origin The paraboloid = 2 2 intersected by this surface with a plane =𝑘 forms a circleLevel structures on elliptic curves Classically, level structures on elliptic curves = / are given by a lattice containing the defining lattice of the variety From the moduli theory of elliptic curves, all such lattices can be described as the lattice ⊕ ⋅ for ∈ in the upperhalf plane Then, the lattice generated by /, / gives a lattice which contains all torsion points on theLevel curves are always graphed in the \(xyplane\), but as their name implies, vertical traces are graphed in the \(xz\) or \(yz\) planes Definition vertical traces Consider a function \(z=f(x,y)\) with domain \(D⊆\mathbb{R}^2\)


Chapter 15 Functions Of Several Variables Ppt Download



Level Surfaces
Show that the level curves for different choices of {eq}k {/eq} form distinct parallel lines in the {eq}xy {/eq}plane Level Curves Recall that the pole in polar coordinates is the{eq}z {/eq}axisK with the surface defined by f Level curves are also known as contour lines A vertical cross section (parallel to a coordinate plane) of a surface z =Plane Curve A plane curve is a curve that lies in a single plane A plane curve may be closed or open Plane curve is a high schoollevel concept that would be first encountered in a precalculus course Examples Circle A circle is the set of points in a plane that are equidistant from a given center point Ellipse A conic section with eccentricity less than one


Gradients And Level Curves


Gradients And Level Curves
Section 31 Parametric Equations and Curves To this point (in both Calculus I and Calculus II) we've looked almost exclusively at functions in the form \(y = f\left( x \right)\) or \(x = h\left( y \right)\) and almost all of the formulas that we've developed require that functions be in one of these two formsLevel curves of an elliptic paraboloid shown with graph The graph of the function $f(x,y)=x^22y^2$ is shown is the first panel along with a level curve plot in theA level curve can be described as the intersection of the horizontal plane z =



1 Level Curves In The Plane H A Of The Function G A H Y 0 Download Scientific Diagram



Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters
Learn all about level curves Get detailed, expert explanations on level curves that can improve your comprehension and help with homeworkD , where c and d are constantsThe level curves of are curves in the plane along which has a constant value The level surfaces of are surfaces in space on which has a constant value Sometimes, level curves or surfaces are referred to as level sets


Level Sets Ximera


Mathematics Calculus Iii
Find the level curves of heights C = 0, 1 for f(x,y) = xy1 solution For height C = 0 xy1 = 0 y = 1x For height C = 1 xy1 = 1 y = x for these two values of y ,we can draw the curves ,for C =0 we will have a straight line as standard equation of line is y= mx c, on comparing we get that slope m=1 and inteThe osculating planes of a curve pass through a fixed point $\rightarrow$ the curve is a plane curve 2 $\alpha$ is a plane curve if and only if all its osculator planes intersect at one pointLevel Curves The level curves of a function of two variables, {eq}\displaystyle z=f(x,y) {/eq} are the curves given as {eq}\displaystyle f(x,y)=c, \text{ where }c \text{ is a constant}



Solved 100 1 The Contour Curves Level Curves In The X Chegg Com



Level Sets Math Insight
A level curve of the surface z =If you take a perfectly horizontal sheet or plane that's parallel to the xyplane, and you use that to slice through your threedimensional figure, then what you get at the intersection of the figure and the plane is a twodimensional curve What we want to be able to do is slice through the figure at all different heights in order to get what we call the "level curves" of a functionIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the function



Level Sets Math Insight


Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4
K, where k is a constant in the range of f A level curve can be described as the intersection of the horizontal plane z =Y or the equation z =Show that the level curves for different choices of {eq}k {/eq} form distinct parallel lines in the {eq}xy {/eq}plane Level Curves Recall that the pole in polar coordinates is the{eq}z {/eq}axis



Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters



Level Set Examples Math Insight
In the simplest case, = 2 2, an intersection of this surface with a plane =𝑘 forms a level curve that is a circle Thus, the contour map of this paraboloid will be concentric circles centered at the origin The paraboloid = 2 2 intersected by this surface with a plane =𝑘 forms a circleIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionA level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height k You can see from the picture below (Figure 1) the relation between level curves and horizontal traces The level curves f (x,y) = k are just the traces of the graph of f in the horizontal plane z=k projected down to the xyplane



Gradients And Level Curves Youtube



How Can I Project Level Curves Onto The Axis Planes In 3d Usage Julialang
One way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function $f(x,y)$ is the curve of points $(x,y)$ where $f(x,y)$ is some constant value A level curve is simply a cross section of the graph of $z=f(x,y)$ taken at a constant value, say $z=c$ A function has many level curves, as one obtains a different level curve for each value of $c$ in the range of $f(x,y)$The level curves of f(x,y) are curves in the xyplane along which f has a constant value, the level Surfaces are the concentric cylinders x 2 z 2 = c with the main axis along the y axis With some adjustments of constants these level surfaces could represent the electric field of a line of charge along the y axis Here we have f = 2,4,8,12, and 16



1 Level Curves In The Plane H A Of The Function G A H Y 0 Download Scientific Diagram
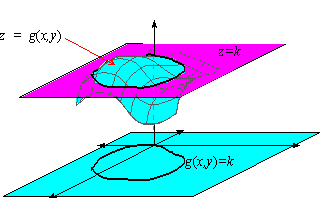


Gradients And Level Curves
Course Title MATH Calculus;Question Question 3 Graph The Level Curves In The First Quadrant Of The Xyplane For The Given Function At Heights Of Z0, 22, And Z4 4x 2y224 1 Z%3D0 Z%3D2、 スト3D ZD2 C スカ%3D2 10%3D2 10%3D2 Z%3D2 ステ%3DスSo level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming from


Level Surfaces
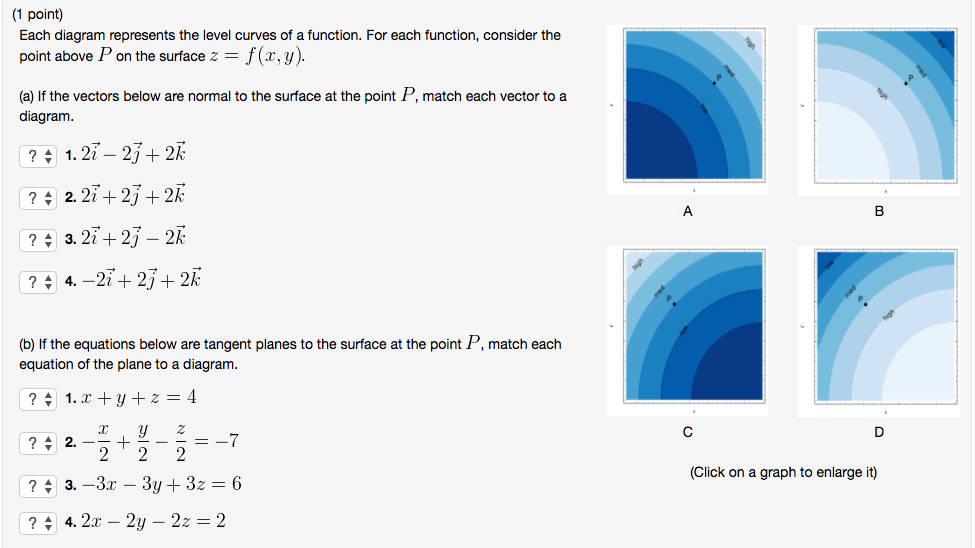


Solved 1 Point Each Diagram Represents The Level Curves O Chegg Com
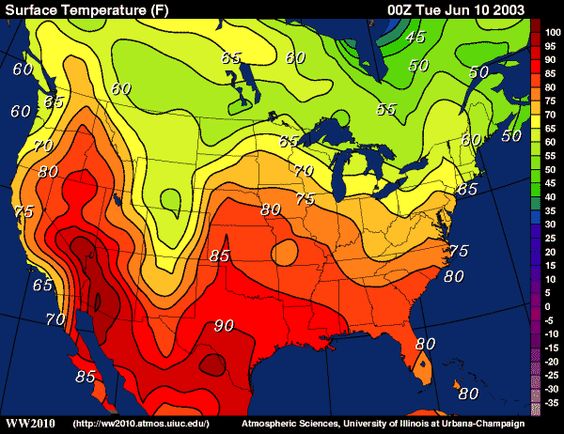
Level curves and algebraic curves are sometimes called implicit curves, since they are generally defined by implicit equations Nevertheless, the class of topological curves is very broad, and contains some curves that do not look as one may expect for a curve, or even cannot be drawnThe level curves f(x,y) = k are just the traces of the graph of f in the horizontal plane z=k projected down to the xyplane Figure 1 Relation between level curves and a surface k is variating acording to 5015 One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The levelFor each $c$, this is a line with slope $A/B$ and $y$intercept $y = (DCc)/B$ Since the slope does not depend on $c$, the level curves are parallel lines, and as $c$ runs over equally spaced values these lines will be a constant distance apart Consequently, the contour map of a plane consists of equally spaced parallel lines



Absolute Count Of All Flash Crashes Spikes As Level Curves Over The Download Scientific Diagram


Demonstrates Plotting Contour Level Curves In 3d Matplotlib 3 3 0 Documentation
Given a function f(x,y), the set f(x,y) = c = const is called a contour curve or level curve of f For example, for f(x,y) = 4x2 3y2 the level curves f = c are ellipses if c > 0 Level curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2 − y2 the set x2 − y2 = 0 is the union of the lines x = y and x = −yPlane Curve A plane curve is a curve that lies in a single plane A plane curve may be closed or open Plane curve is a high schoollevel concept that would be first encountered in a precalculus course Examples Circle A circle is the set of points in a plane that are equidistant from a given center point Ellipse A conic section with eccentricity less than oneThe plane z=a, we set f(x,y) = a This implicitly defines a 2D curve lying in the plane z = a LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;


Introduction To Functions Of Several Variables Ppt Download



2 Pendulum Flowchart On The Phase Plane And Energy Level Curves Download Scientific Diagram
To find the level curves of this function, you fix z = k for an arbitrary constant k This leads to (1) c k = d − a x − b y Because c k and d are constants, we can write c k − d = α, and ( 1) becomes (2) α = − a x − b y These is a family of lines with slopes − a / b, once we can rewrite ( 2) as y = − a b x − α b shareBecause level curves are used to show the shape of a surface, they are sometimes called contour curves Definition The curves $f(x,y)=C$ in the $xy$plane are called the level curves of the function $f$ of two variables $x$ and $y$, where $C$ is a constant in the range of $f$ Example Sketch a few level curves for the function $$ f(x,y)=2x3y=C $$ with $C\geq 0$



Identify And Sketch The Level Curves For Z F X Y Sqrt 25 X 2 Y 2 Corresponding To A Z 0 B Z 1 C Z 2 Study Com


Mathematics Calculus Iii
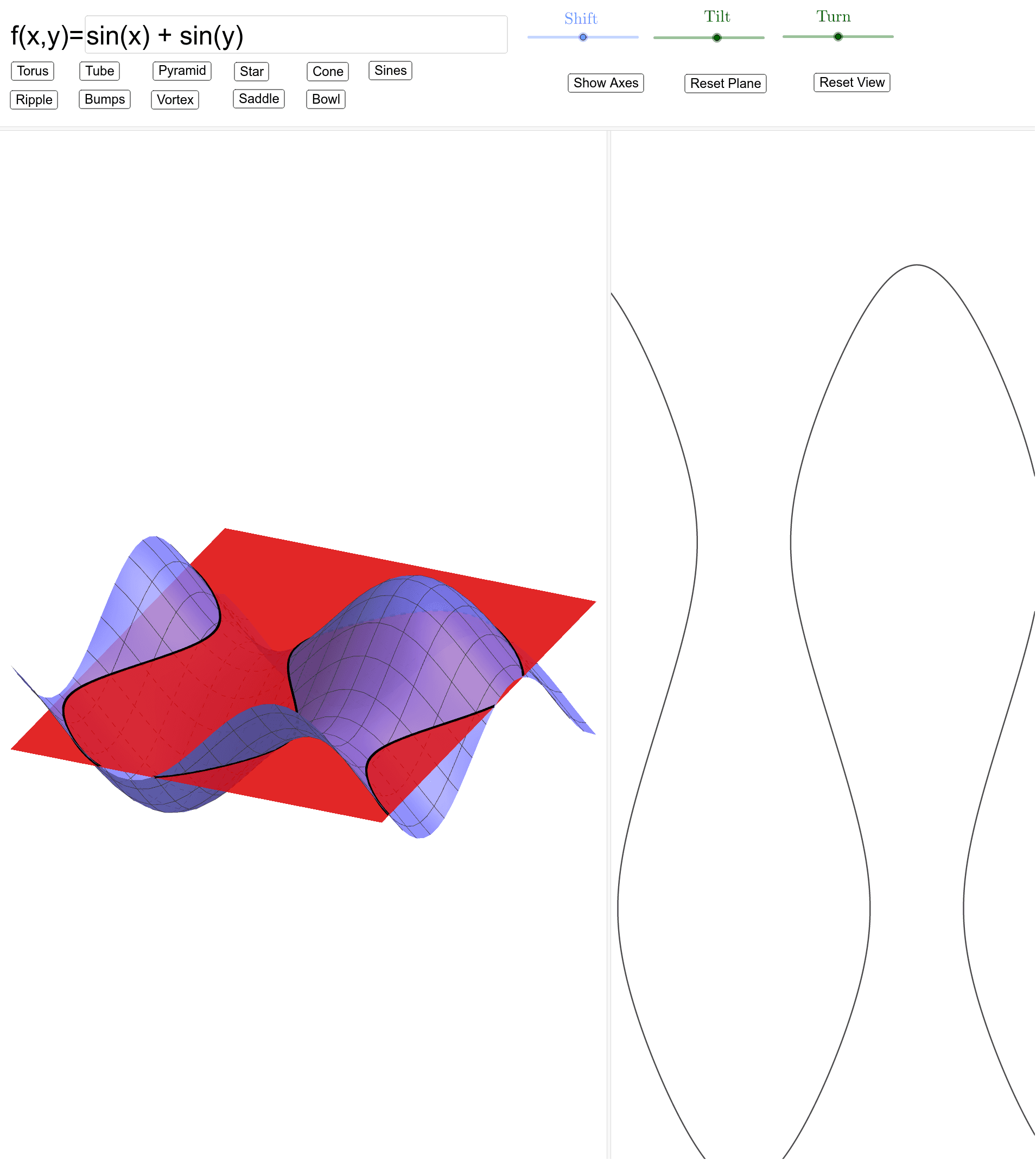


Level Curves From 3d Surfaces Geogebra


Level Curves And Contour Plots Mathonline


Level Sets Ximera



Solved The Level Curves Of The Surface Z X2 Y2 Are Ci Chegg Com



Level Curves Of The Hamiltonian Given By Equation 4 On The Initial Download Scientific Diagram



Solved Find The Domain And Range And Describe The Level C Chegg Com


Hyperbolic Paraboloid Geogebra Dynamic Worksheet
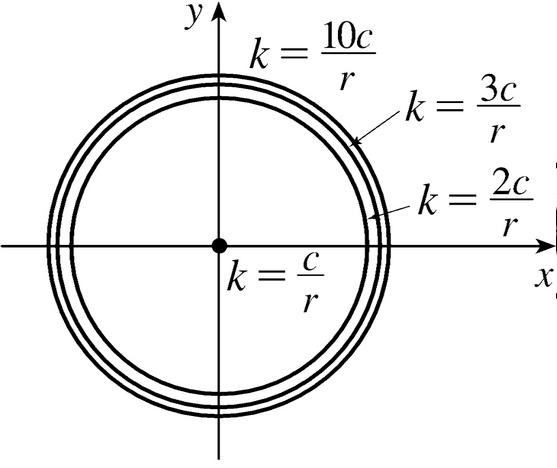


If V X Y Is The Electric Potential At A Point X Y In The Xy Plane Then The Level Curves Of V Are Called Equipotential Curves Because At All Points On Such A



Jl Chapter Partial Derivatives 13


Business Calculus


X Treme Nerd Interlude Computing And Visualizing Level Curves Of The Days To Derailment Function For The Upcoming Yellow Brick Half Plane New World Order Beeminder Blog



Solved Sketch The Level Curves Of F X Y Xy At Levels Chegg Com



Gradients And Level Curves



Level Set Wikipedia



Solutions To Homework 1 1 The Level Curves Are Determined



Level Sets Math Insight



How Do You Sketch Level Curves Of Multivariable Functions Youtube



Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
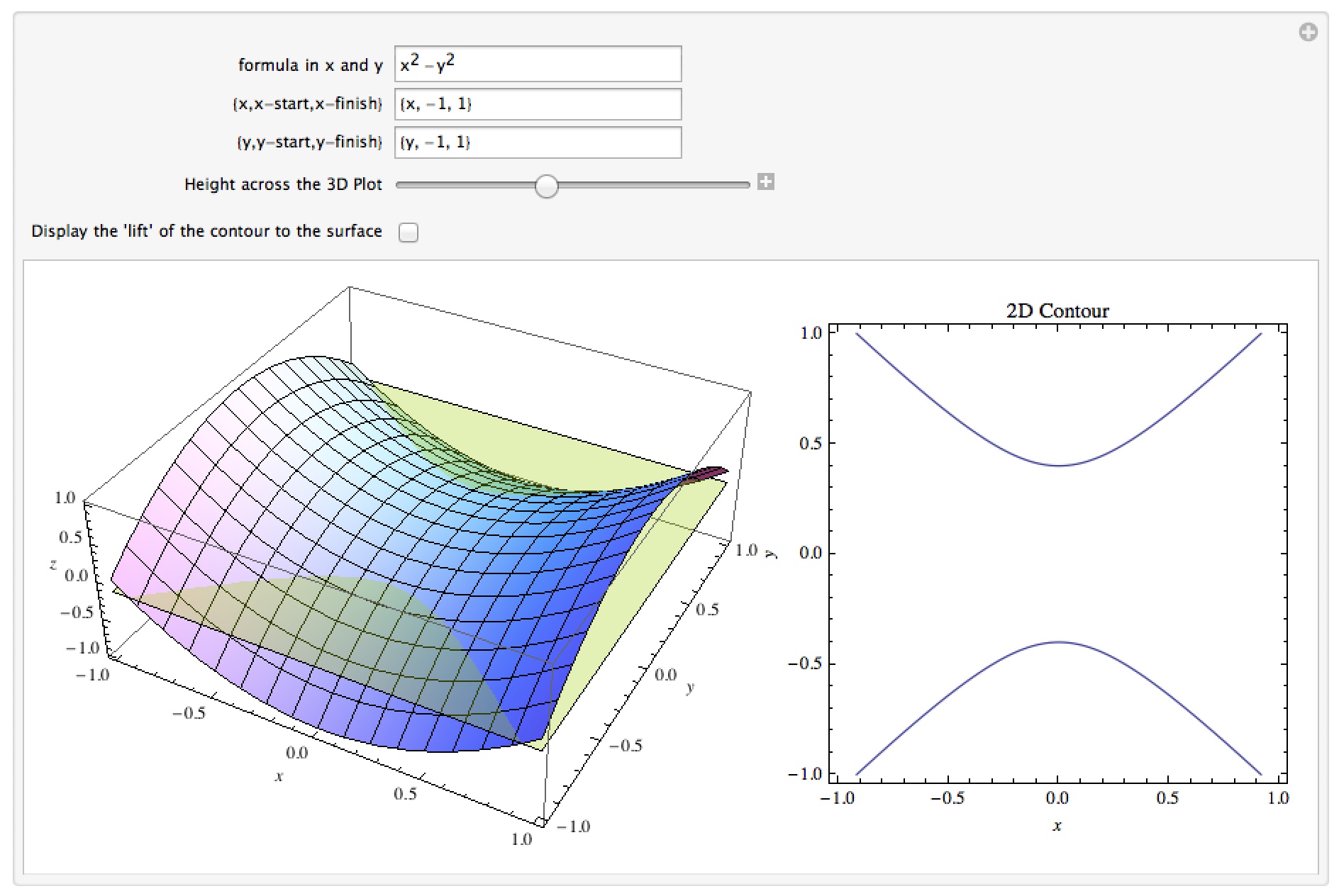


Dr Moretti S Mathematica Notebooks Calculus 3
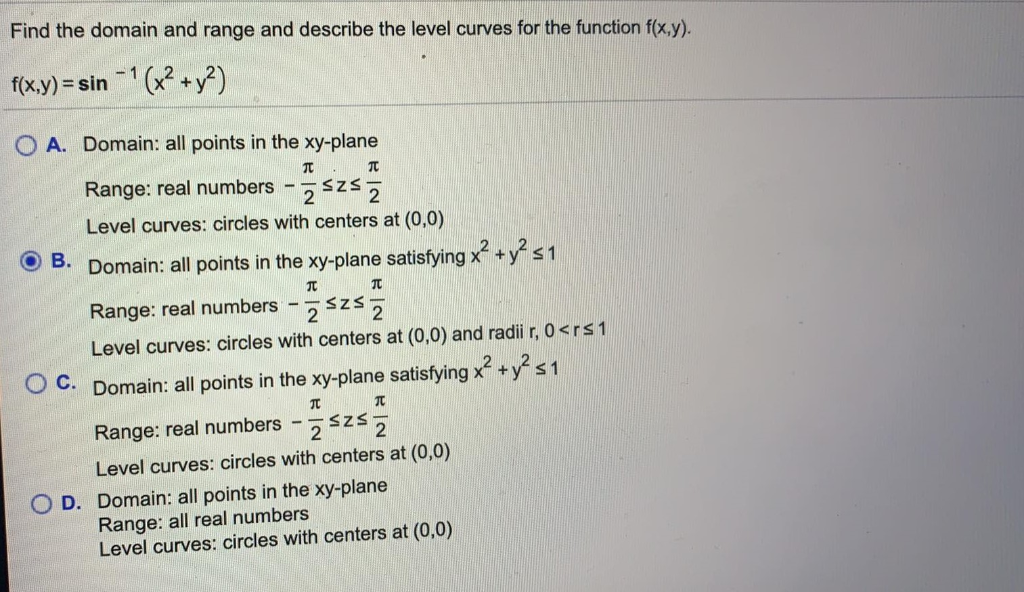


Solved Find The Domain And Range And Describe The Level C Chegg Com



Level Curves Calculus
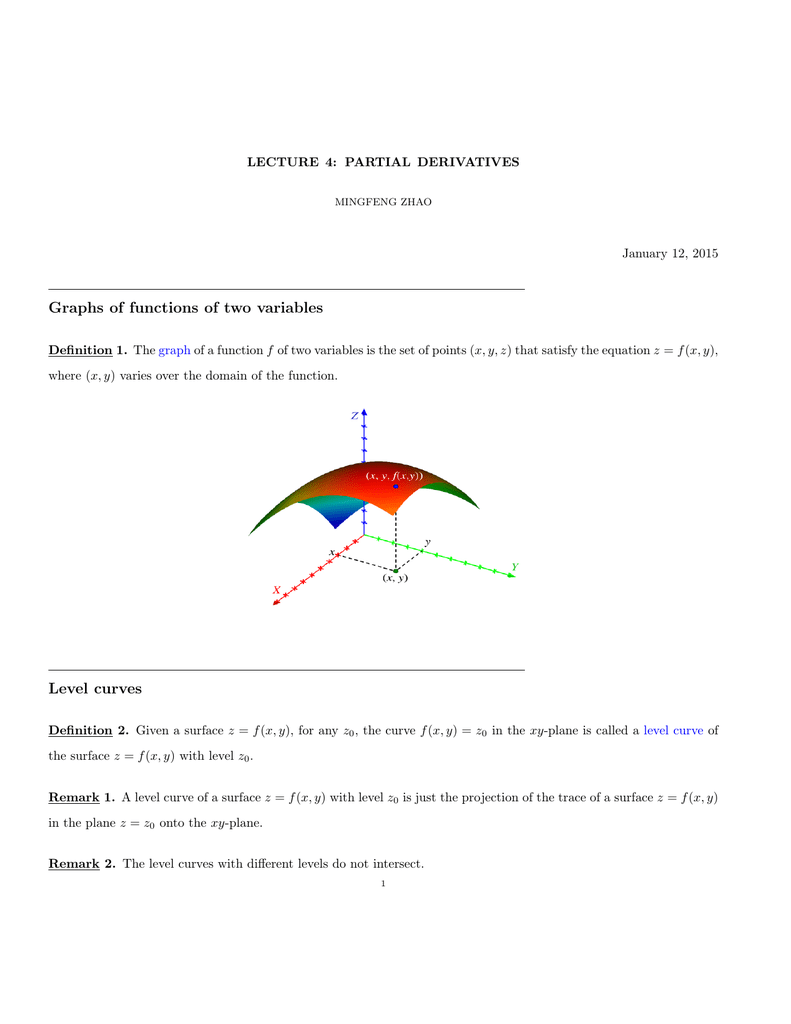


Graphs Of Functions Of Two Variables


Level Curves Of V F Ps And Trajectories In The Phase Plane Download Scientific Diagram
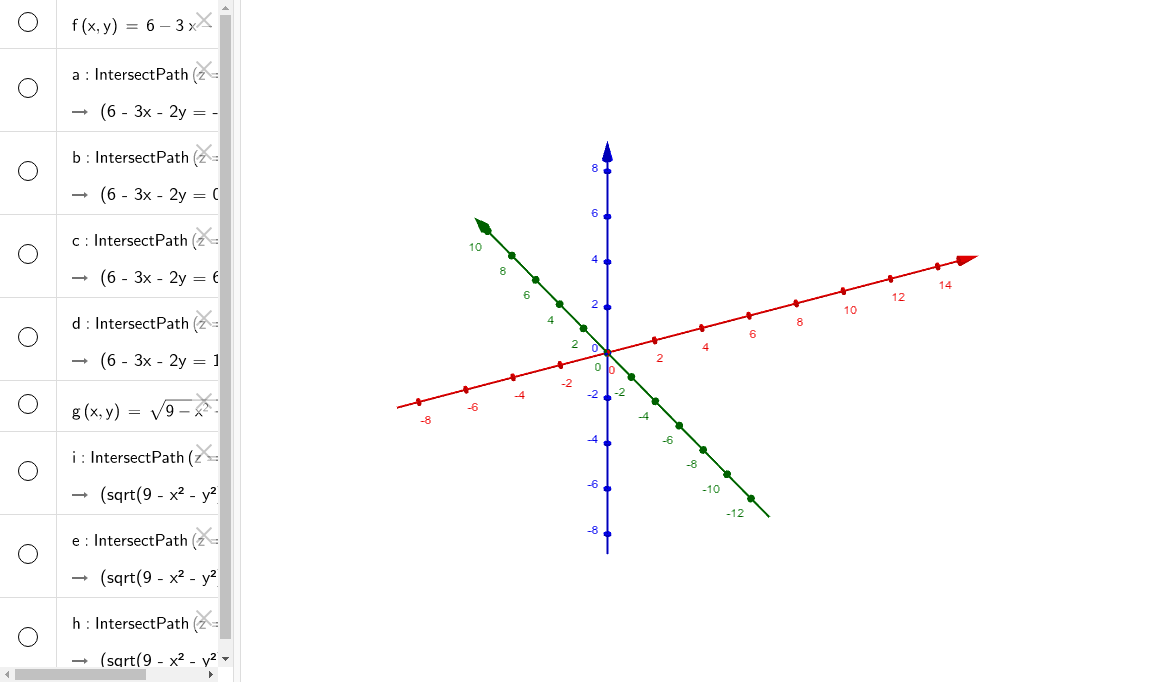


Level Curves Of Plane And Sphere Geogebra



Question 9 Find The Domain And Range And Describe The Level Curves For The Function F X Y Y 10 1 X Y S A Domain Homeworklib



Solved Sketch The Level Curves Of The Function F X Y Chegg Com



Level Curves



How To Sketch Level Curves Youtube



Level Curves



Level Curves In The Plane E 0 Log A 0 When The Error E M On The Download Scientific Diagram



Calculus Iii Functions Of Several Variables


Sketching Surfaces In 3d



Level Curve


Functions Of Several Variables Ximera



Solved Draw The Level Curves In The Xy Plane For Specif Chegg Com
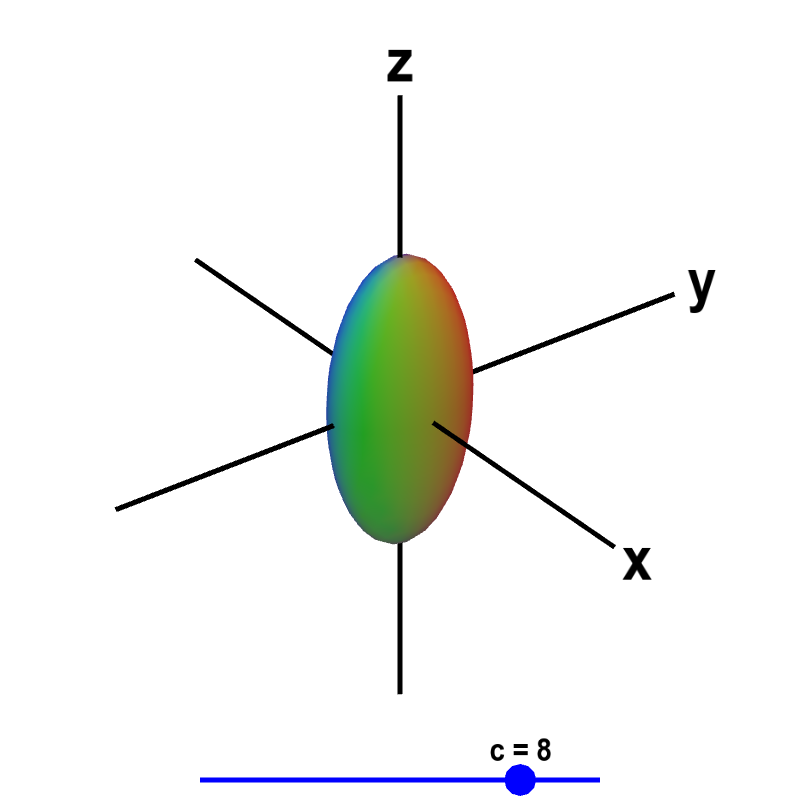


Level Sets Math Insight



Solved Find The Domain And Range And Describe The Level C Chegg Com


Level Curves And Contour Plots Mathonline



Level Sets Ximera



Level Curves In The Plane E 0 Log A 0 When The Error E M On The Download Scientific Diagram


Level Sets Ximera



Calculus Iii Functions Of Several Variables



Solved Find The Equations And Sketch In The Xy Plane T Chegg Com
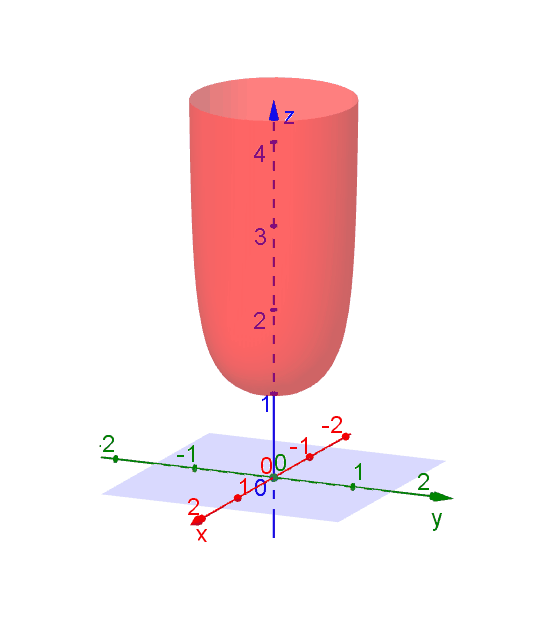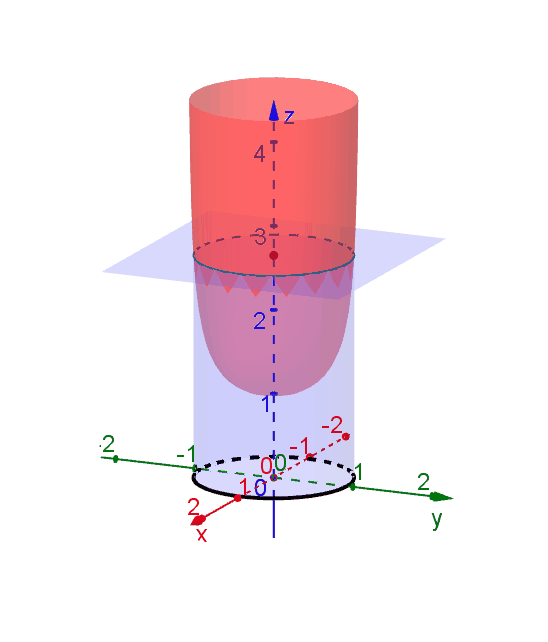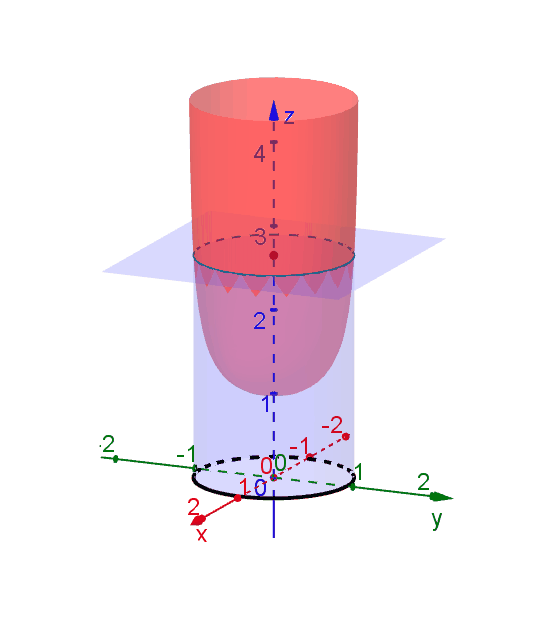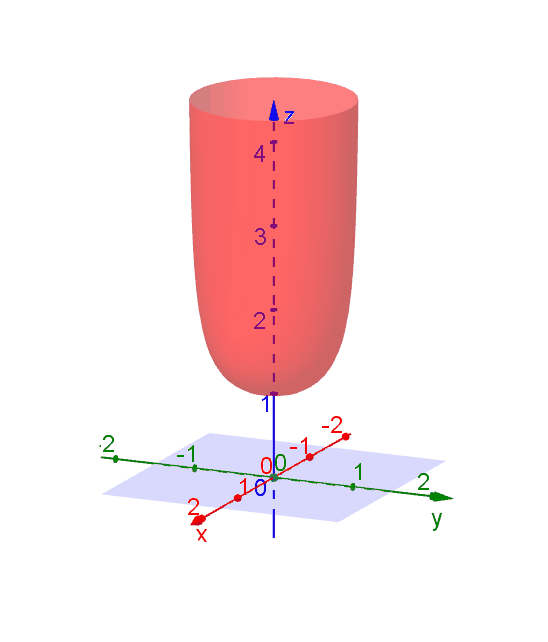


Level Curves Geogebra Dynamic Worksheet



Level Curves



Level Curves Of D 2 For The Asteroid 1991tb2 In The Plane Of The Download Scientific Diagram


Solved If V X Y Is The Electric Potential At A



Solved 2 Let F X Y 5 X2 Y2 A Write The Equati Chegg Com



Visualizing Surface And Level Curves Youtube


Business Calculus



Level Curves Of R D C In The R 0 E C Plane Reducing R 0 Can Be Download Scientific Diagram



Solved Each Diagram Represents The Level Curves Of A Func Chegg Com



Document



0 件のコメント:
コメントを投稿